問題を解きたい方向け:ネタバレを含みます。
1回間が空いてしまいましたが参加してきました。今回は時間内に解けなかったのですが、問題的にプログラミングせずに解けるんじゃないかという気がしたのでほとんどプログラミングせずに解いた結果のwriteupをお届けします。
普通に解いたらこうなる
ヘルパーメソッド的なのがそのまま残ってたりあってるかどうかの確認部分が全部コメントアウトになっていたりというところは目をつぶるとして…
- まずは指定された状況まで盤面を作る(solveの再帰、apply)
- できた盤面を左上から順に白を探し、連続した白を塗って数え上げていく(paint_board)
- paint_boardも再帰で書いていたけどあるところからstack size exceededと言われたのでqueueを用いて書き直した
…というのがやってる中身。
これ、「数学の問題として」解くことができるのでは?
現場でも思って結局間に合わなかったのですが、ある状態に対して操作を適用して新しい状態を作る、という過程でその状態の中の特徴的な値を計算する、というのであれば、最終的な盤面を作って数え上げる、ということをせずとも適切なモデリングをすれば漸化式で解くことができるのでは?と思って、解散後からその方針で解答を準備しました。
Oの連続のケース
まずは「Oの連続数をnとして、できる領域数をnを用いて表せ」という小問題を解きます。
詳細な証明は省略しますが、以下の要領で白の領域を数え上げます:
- 対角線で正方形を分割し、そのうちの1つの三角形の状態をn=1の状態(1個の空白のある状態)に対応づける。
- n=2の状態として、その三角形から図のように小さい三角形を2つ作った状態とする。
- n=3以降では、前の状態の最も小さい三角形からさらに2つの小さい三角形を作る。
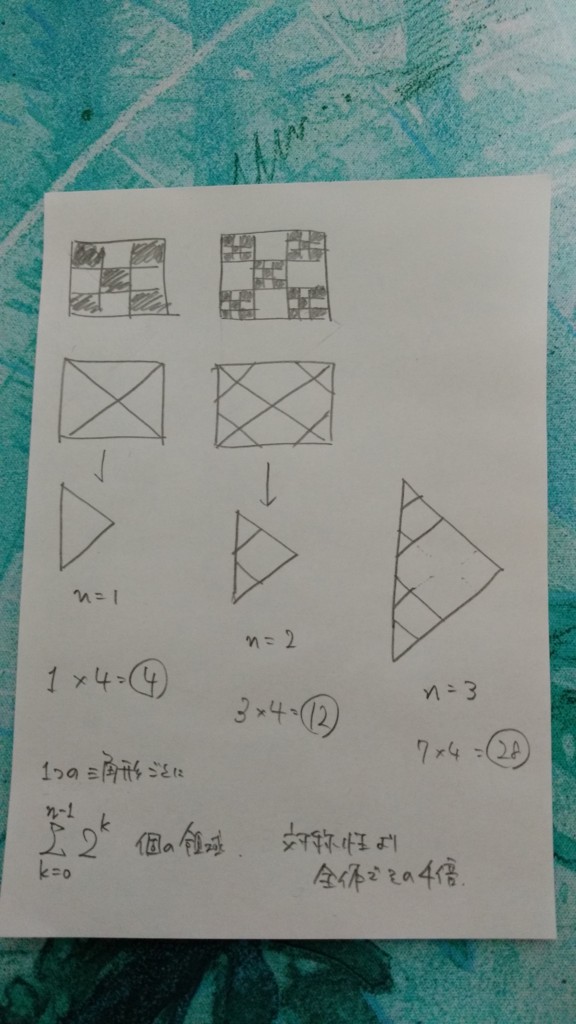
これによって、Oの連続のときは 2n+3 - 4 個の領域ができます。
Xの連続のケース
ここから少々厄介です。Xの連続数をnとしたとき、n=1のときとn=2以上のときとで計算方法が変わります。n=1のときは見たまんまで領域数5です。
Xという操作は以下のような性質を持ちます:
- 隣接した黒のマスを作らない。(これはOについても同様なので、任意の回数OとXを繰り返したとき隣接した黒のマスは生じない)
- [[0,1],[1,0]]のような形で黒と白が並んでいるとき(0が黒でも1が黒でもどちらでもよい)、これにXを適用すると前の状態では別の領域として数えられていた白地は適用後には1つの白地になる。(これがn=2以上で場合分けが必要な理由)
- 上記の性質より、n=2以上のときn=1時に存在する中央の白地と角の白地は全部くっつく。
- n=2以上で、黒のマスにXを適用すると間に新規に1つの白地ができる。
最後の性質から、n回Xを適用したときの白地の数は(前の黒のマスの数) + 1となり、
- 黒のマスの数はn=1で4
- Xを1回適用するごとに4倍
以上より、n >= 2 で 4n-1 + 1 個の白地が存在することになります。
OとXの混合ケース
Xで終わる場合
Xで終わる場合、Xのみのケースと同様、前の黒のマスの数を用いて計算できるので、
- Xは黒のマスを4倍する
- Oは黒のマスを5倍する
ことから、Xの数をn、Yの数をmとして、4n-1 * 5m + 1 個、と計算できます。 しかし、Xが1個の場合(Oの連続のあとにXが来る場合)は例外があり、「Oのみの連続の場合は角は黒」「Xが初めて来ると角に白ができる」…ということで角の4つの白地も数えてあげなくてはいけなくなり、このときは 41-1 * 5m + 1 + 4、つまり 5m + 5が求める領域数になります。
Oで終わる場合
Oという操作の性質として、
- 操作前に存在した白地の数は保存される
- その上で、辺もしくは角に接する黒が新規の白地を作る。辺に接する黒マス1つが1つ、角の黒マスが2つの白地を新規に作る
- このとき、「OとXが混合」かつ「Oで終わる」ので「角は必ず白」であることに注意
という性質があります(証明はちゃんとしたの書ける気がしないので省略。おそらく「隣接する黒は存在しない」という性質とセットで扱うと「白地が減らない」は証明できそう)。
以上より、前の状態の白地の数 + 新規にできる白地の数、で計算できることになります。
新規にできる白地の数は辺に接する黒マスの数に等しく、それは
- Xは辺に接する黒を増やさない
- Yは辺に接する黒を2倍する
- 初期値は4
…なので、結果として 前の状態の白地の数 + 2m+1 *1で与えられます。
直接計算するコード
以上の結果を用いたのがこちらになります。…結局プログラム使って検証してるやん、ってのはナシで!
もっとマシな書き方ができるかもしれませんがこんなところですかね…。あとOとXの混合ケースをわざわざ再帰せずにもっと簡潔に書く方法があるかもしれない。
感想
時間内で数学の問題として解く解法にたどり着いた人もいたみたいだし、数学が得意な人なら数学で解く解法、そうでない人はがんばれば1時間以内にプログラミングできる、という意味で非常にバランスの取れた問題だったのでは、という印象。なお私は解けませんでした。1文字ずつ適用するなら再帰で解きたい、となってmulti-body functionがほしいからElixirで書き出したものの、多次元配列をうまく扱う方法を知らず苦戦し結果として時間切れ、その後は諦めてRubyで書いた。次から多次元配列使ったりvector使ったりする問題はD言語とかで解こう…。